# Chapter 2. Classical Physics from Newton to Einstein
# 2.1. The scientific method
The scientific method has five major components:
- The assumption of an external, objective reality that can be observed.
- Quantitative experiments on the external, objective reality in order to determine its observable properties, and the use of induction to discover its general principles. This was first systematically articulated by English statesman Francis Bacon (1561–1626) in his Novum Organum, published in 1620.
- Analysing quantitative experiments with mathematical precision. Italian scientist Galileo Galilei (1564–1642) is thought to be the first to clearly state that the laws of nature are mathematical. He has been variously called the “father of modern observational astronomy”, the “father of modern physics” and the “father of modern science”. In his 1632 book, Dialogue Concerning the Two Chief World Systems, he argued for the Copernican model of the solar system against the traditional Ptolemaic system.
- Validation of the results of experimental measurements by widespread communication and publication so that other scientists are able to verify them independently. Although scientists throughout history have communicated and published their results, the first scientist to articulate the need for publishing the details of his experimental methods so that other scientists could repeat his measurements was English chemist Robert Boyle (1627–1691), who was strongly influenced by the views of Bacon.
- Intuiting and formulating the mathematical laws that describe the external, objective reality. The most universal laws are those of physics, the most fundamental science. English natural philosopher Isaac Newton (1642–1727) was the first scientist to formulate laws that were considered to apply universally to all physical systems.
The last four of these components (three of them by Englishmen!) were all developed in the remarkably brief period from 1620 to 1687.
# 2.2. Newton’s laws and determinism
In order to understand quantum physics, we must first understand classical physics so that we can see the differences between them.
There are two fundamental assumptions in classical physics. The first fundamental assumption is that the objective world exists independently of any observations that are made on it.
To use a popular analogy, a tree falling in the forest produces a sound whether or not it is heard by anyone. While it is possible that observations of the objective world can affect it, its independence guarantees that they do not necessarily affect it.
Questions
How might our lives be different if there were no external objective reality but we did not know it?
What if we did know it?
The second fundamental assumption of classical physics is that both the position and velocity of an object can be measured with no limits on their precision except for those of the measuring instruments. In other words, the objective world is a precise world with no intrinsic uncertainty in it.
As we shall see later, quantum theory abandons both of these fundamental assumptions.
Isaac Newton was the first important scientist both to do fundamental experiments and to devise comprehensive mathematical theories to explain them. He invented a theory of gravity to explain the laws of German astronomer and mathematician Johannes Kepler (1571–1630) which describe the planetary orbits, made use of the famous free-fall experiments from the leaning tower of Pisa by Italian scientist Galileo Galilei (1564–1642) and invented the calculus in order to give a proper mathematical framework to the laws of motion that he discovered. Newton considered himself to be a natural philosopher, but contemporary custom would accord him the title of physicist. Indeed, he, probably more than any other scientist, established physics as a separate scientific discipline because of his attempts to express his conclusions in terms of universal physical laws. He is thought by some to have been the greatest scientist that has ever lived. In 1687 at the age of 44 he published his Philosophiæ Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy) in which he set forth his laws of motion and gravitation.
His three laws of motion can be written as follows:
- A body moves with constant velocity (speed and direction) unless there is a non-zero net force acting on it. (A body at rest has a constant zero velocity, thus the net force acting on it must be zero.)
- The rate of change of the velocity (change in speed or direction, called the acceleration) of a body is proportional to the force on the body.
- If one body exerts a force on another body, the second body exerts an equal and opposite force on the first.
In order to use these laws, the properties of the forces acting on a body must be known. As an example of a force and its properties, Newton’s law of gravitation states that the gravitational force between two bodies, such as the earth and the moon, is proportional to the mass of each body and is inversely proportional to the square of the distance between them. This description of the gravitational force, when used together with Newton’s second law, explains why the planetary orbits are elliptical. Because of Newton’s third law, the force acting on the earth is equal and opposite to the force acting on the moon. Both bodies are constantly changing their speeds and directions because of the gravitational force continually acting on them.
Another example is the gravitational force acting between the earth and my body. Whenever my body is stationary, there must be another force acting on it, otherwise Newton’s first law would not be correct. If I am sitting on a chair, this other force is an upward force acting on my body by the chair, and this just cancels the gravitational force acting on my body by the earth. The force acting on my body by gravity (my weight) is equal and opposite to the force acting on my body by the chair, and vice versa.
Question
What is our most immediate sensation of the gravitational force?
What if we are in free fall?
Question
What are the forces on a car if it is accelerating straight ahead?
If it is moving with constant speed in a circle?
For more than two hundred years, after many experiments on every accessible topic of macroscopic nature, Newton’s laws came to be regarded by physicists and by much of society as the laws that were obeyed by all phenomena in the physical world. They were successful in explaining all motions, from those of the planets and stars to those of the molecules in a gas. This universal success led to the widespread belief in the principle of determinism, which says that, if the state of a system of objects (even as all-encompassing as the universe) is known precisely at any given time, such as now, the state of the system at any time in the future can in principle be predicted precisely. For complex systems, the actual mathematics might be too complicated, but that did not affect the principle. Ultimately, this principle was thought to apply to living beings as well as to inanimate objects. Such a deterministic world was thought to be completely mechanical, without room for free will, indeed without room for even a small deviation from its ultimate destiny. If there was a God in this world, his role was limited entirely to setting the whole thing into motion at the beginning.
Intrinsic to the principle of determinism was the assumption that the state of a system of objects could be precisely described at all times. This meant, for example, that the position and velocity of each object could be specified exactly, without any uncertainty. Without such exactitude, prediction of future positions and velocities would be impossible. After many, many experiments it seemed clear that only the inevitable imprecision in measuring instruments limited the accuracy of a velocity or position measurement, and nobody doubted that accuracies could improve without limit as measurement techniques improved.
Question
How might our lives be different if the world were deterministic but we did not know it?
What if we did know it?
Questions
Suppose you accepted the principle of determinism as truth. How would you then feel about your feelings, decisions and actions? About other people’s feelings, decisions and actions? How would it affect your judgements about yourself and others?
# 2.3. Thermodynamics and statistical mechanics; entropy and the direction of time
Thermodynamics is the physics of heat flow and of the interconversion between heat energy and other forms of energy. Statistical mechanics is the theory that describes macroscopic properties such as pressure, volume and temperature of a system in terms of the average properties of its microscopic constituents, the atoms and molecules. Thermodynamics and statistical mechanics are both concerned with predicting the same properties and describing the same processes, thermodynamics from a macroscopic point of view, and statistical mechanics from a microscopic point of view.
In 1850, the German physicist Rudolf Clausius (1822–1888) proposed the first law of thermodynamics, which states that energy may be converted from one form to another, such as heat energy into the mechanical rotation of a turbine, but it is always conserved. Since 1905 when German-Swiss-American physicist Albert Einstein (1879–1955) invented the special theory of relativity, we know that energy and matter can be converted into each other. Hence, the first law actually applies jointly to both matter and energy. This law is probably the most fundamental one in nature. It applies to all systems, no matter how small or large, simple or complex, whether living or inanimate. We do not think it is ever violated anywhere in the universe. No new physical theory is ever proposed without checking to see whether it upholds this law.
Question
What are some everyday examples of the first law of thermodynamics?
The second law of thermodynamics can be stated in several ways. The first statement of it, made by Rudolf Clausius in 1850, is that heat can flow spontaneously from a hot object to a cold object but it cannot spontaneously pass from a cold object to a hot object. The second statement of the second law was made later by Scottish physicist William Thomson Kelvin (1824–1907) and German physicist Max Planck (1858–1947): Heat energy cannot be completely transformed into mechanical energy, but mechanical energy can be completely transformed into heat energy.
Question
What are some everyday examples of the second law of thermodynamics?
The third statement of the second law depends on a new concept, that of entropy. In order to discuss entropy, we first discuss the number of distinguishable arrangements of a system, from which the concept of entropy is derived. Some readers may wish to skip this discussion and go directly to the definition of entropy that is given afterwards.
Example #1: Imagine a box divided into two compartments, each of which can hold only one ball. Put a ball into one of the compartments. Clearly, the number of ways that you can do this is two — the ball can be put into either compartment. (Mathematically, this is the number of combinations of two objects taken one at a time; this is given by the binomial coefficient).
Example #2: If there are three compartments, the number of ways you can put a ball in is three (the number of combinations of three objects taken one at a time).
Example #3: If there are four compartments, the number of ways you can put a ball in is four (the number of combinations of four objects taken one at a time).
Example #4: Now put two identical balls into a box with two compartments. The number of ways you can do this is only one (the number of combinations of two objects taken two at a time) because if the balls are interchanged, there is no distinguishable difference in the arrangements.
Example #5: Now put two identical balls into a box with three compartments. The number of ways you can do this can be counted in the following way:
- The first ball in compartment #1, the second in either of the other two. This adds up to two.
- The first ball in compartment #2, the second in either #1 or #3. But the first arrangement is identical to the first arrangement of (a), so we don’t count it. The second arrangement is new, so we count it. If now the first ball is now put into #3, the second can be put into either #1 or #2, but these are not new, so we don’t count them.
Thus, the total number of distinguishable arrangements for two identical balls in three compartments is three (the number of combinations of three objects taken two at a time).
Example #6: Now put two identical balls into a box with four compartments. We count the number of possible ways as follows:
- The first ball in #1, the second in #2, #3, or #4. This adds up to three.
- The first ball in #2, the second in #1, #3, or #4. The first is the same as the first arrangement of (a), so there are two new distinguishable arrangements.
- The first ball in #3, the second in #1, #2, or #4. Only the last arrangement is new, so there is one additional distinguishable arrangement. 4.The first ball in #4, the second in #1, #2, or #3. Each of these arrangements is identical to (a), (b) or (c), so these are not new.
Thus, the total number of distinguishable arrangements for two identical balls in four compartments is six (the number of combinations of four objects taken two at a time).
Example #7: Now put two balls into only the first three of four compartments. This is identical to Example #5 except that now there are two balls in four compartments instead of two balls in three compartments. The number of distinguishable arrangements is now three as long as we know that the balls are in the first three compartments. This example shows that the number of distinguishable arrangements depends not only on the number of balls and compartments, but also on how the balls are distributed in the compartments.
The methods of probability allow us to calculate the number of distinguishable arrangements in any number of compartments whether the balls are identical or not, and for any given distribution of balls. For a given number of compartments and for identical balls, the number of distinguishable arrangements is smallest (equal to one) when the number of balls is the same as the number of compartments (example #4). This would correspond to a pure crystalline solid material. For a given number of compartments and identical balls, the number of distinguishable arrangements is maximum when the number of balls is equal to half the number of compartments (example #6). This would correspond to a highly compressed gas. For a rarefied gas, the number of compartments (each equal to the size of a molecule) is vastly larger than the number of molecules, and the number of distinguishable arrangements is much greater than one (example #3) but less than the maximum (example #6).
We are now able to define entropy. Entropy is related to (actually, is proportional to the logarithm of) the total number of distinguishable possible arrangements of the system (in a six-dimensional position–velocity space — three dimensions for position and three for velocity — rather than in the three-dimensional position space of the example above). Entropy quickly increases as we increase the volume of the system, the number of objects in it, and the total energy of the objects. For a macroscopic system, say of 1023 particles, the entropy is enormously larger than for the system of two balls described above. Entropy also is larger when the objects are uniformly distributed (example #6) than when they are clumped together (example #7). It turns out that it is also larger when energy as well as mass is distributed uniformly. Since energy is related to temperature, entropy is larger when the temperature is uniform, and it increases when the temperature increases.
Entropy is related to the amount of disorder and order in the system. Decreasing entropy is equivalent to decreasing disorder or disorganisation (increasing order or organisation) of an object or system (example #7); while increasing entropy is equivalent to increasing disorder or disorganisation (decreasing order or organisation) (example #6).
It turns out that the second law of thermodynamics can be stated in the following way: Natural processes of an isolated macroscopic system normally proceed in the direction of maximum probability (maximum disorder), which is the direction of maximum number of distinguishable arrangements of the system. (It is highly improbable, although not totally impossible, for them to proceed in the opposite direction.) The forward direction of time is the direction in which entropy increases. Thus, the second law of thermodynamics can be restated in terms of entropy: Natural processes of an isolated macroscopic system always proceed in the direction of increasing entropy (disorder). In classical physics, this defines the forward direction of time. In Section 6.4, we shall see what determines this direction in quantum physics. (Note that we have emphasised that the second law applies only to a system that is isolated from the rest of the universe, or to the universe as a whole.)
The second law is based on our observations of the direction in time of natural processes. We say that this direction depends on the universe proceeding in time from a state of lower entropy to a state of higher entropy but, in classical physics, the increasing direction of entropy is identical to the forward direction of time. We cannot distinguish one from the other. It is tautological to say that entropy increases with time because the increase of entropy cannot be distinguished from the forward direction of time. However, in quantum physics, the direction of time is determined by the nature of a quantum event (see Chapter 6).
Note
The fact that the forward direction of time is the direction of increasing entropy implies that the universe began in a much lower entropy state than that of today. What caused the entropy to be so low when the universe began is not known. This is a subject of intensive research in theoretical cosmology.
The direction of time can also be inferred from the first two statements of the second law of thermodynamics: 1) The unidirectional flow of heat from hot to cold bodies, and 2) the possibility of total conversion of mechanical energy to heat energy, but not the reverse.
A mistake made by some people is to think that the second law applies to individual objects or systems, such as automobiles, plants or human bodies, even if they are not isolated from the rest of the universe, and that this is the reason that such objects decay and disintegrate with time. This is a fallacy, however, because the second law does not prevent the entropy of an individual object from continuously decreasing with time and thus becoming more ordered and organised as long as it receives energy from something else in the universe whose entropy continues to increase. In our solar system, it is primarily the sun’s entropy that continually increases as its fuel is burned and it becomes more disordered.
The above discussion is based on our understanding of objective time within classical physics. It says nothing about our subjective sense of the passage of time. Regardless of what the clock says, everybody experiences time as passing faster in some circumstances than in others. Our experience of duration depends on our perception of the degree of change and on our accompanying emotional state (“Time flies faster when you’re having fun”; “How time flies!”).
Question
Do you think that the entropy of your body is decreasing as you get older, or is it increasing?
Economist Jing Chen has written that natural selection in biological evolution can be seen as a force towards low entropy states of the human mind at the cost of increasing entropy of the universe:
People generally think that physical laws only have limited utility in understanding human behaviour because our mind is free. However, human mind is shaped by natural selection and sexual selection. Living organisms need to extract low entropy from the environment, to defend their low entropy sources and to reduce the diffusion of the low entropy. The struggle to stay in low entropy states is called natural selection. In human societies, agriculture is the main low entropy source. Part of health care systems aim at defending our own low entropy sources to be accessed by viruses and bacteria. The military forces are established to extract low entropy from others and to defend own low entropy sources. Clothing and housing reduce the diffusion of low entropy.
Sexual selection is the struggle between the individuals of one sex, generally the males, to communicate their attractiveness to the other sex in order to form a partnership for reproduction. Human beings, as well as other sexually reproducing species, are the successful descendants of the earliest sexually reproducing species about a billion years ago. For the system of communication to be successful in different kinds of environments over such a long time, the mode of communication has to be simple, stable and universal. Since the entropy law, which states that closed systems tend towards states of higher entropy, is the most universal law of the nature, it is natural that the display of low entropy levels evolves as the universal signal of attractiveness in the process of sexual selection.
As both natural selection and sexual selection favour low entropy state, the pursuit of low entropy becomes the main motive of human mind and animal mind. Indeed the low entropy state is the main way of advertisement for most sexually reproducing species. Large body size, colourful and highly complex feather patterns with large amount of information content and exotic structures are all different representations of low entropy states. Since a low probability event corresponds to a state of low entropy, a novel feature is often attractive in the competition for reproduction. It has been generally recognised that sexual selection is the main drive of diversity.
Besides communication with members of the opposite sex, social animals need to communicate their attractiveness and power in order to influence the behaviour of others. For the same reason as in sexual selection, the most general signal is display of low entropy. Among all social species, human beings have developed the most complex social structure. The creation of distinct art works, the demonstration of athletic prowess, the accumulation of wealth, and conspicuous consumption — all of which represent different forms of low entropy — are the major methods of advertising one’s attractiveness.
As the social groups become larger and the division of labour becomes finer, people become less familiar with each other in their daily interactions, which make it more difficult for people to judge the ability of others. The need for people to advertise their attractiveness through external accumulation of low entropy also becomes stronger. People usually signal their capability by buying more expensive houses, cars, clothes, going to more expensive restaurants and attending more exclusive schools. The great efforts human beings put into non-food activities reflect the high cost of communication in a large and complex society. Historical evidences show that the transaction costs have been increasing over time.[1]
The “transaction costs” that Chen speaks about mean that the struggle to achieve and sustain localised low entropy states leads to higher entropy in the universe as a whole.
Question
In your own life, how do you experience the struggle to achieve and sustain low entropy states? What are the transaction costs of this struggle, i.e., in what way does your struggle increase the overall entropy of the world? How successful have you been in your efforts to achieve and maintain low entropy states? How sustainable are such states?
An extremely important property of Newton’s laws is that they are time reversal invariant. What this obscure-sounding term means is that, if the direction of time is reversed, the directions of motion of all particles are also reversed, and this reversed motion is completely allowed by Newton’s laws. In other words, the motion in reversed time is just as valid as the motion in forward time, and nature herself does not distinguish between the two. A simple example of this is the time-reversed motion of a thrown baseball, which follows a parabolic trajectory in either the forward or the reversed direction. Without seeing the act of throwing, and without air resistance, we would not be able to distinguish the forward parabola from the reversed parabola. Another way to state it is that a movie of a thrown baseball seems just as valid to us if it is run in the reverse direction as in the forward direction. Time reversal invariance is also apparent in the seemingly random motion of the molecules in a gas. If we could see their motion in a movie and then reverse it, we could not distinguish between the forward motion and the reversed motion.[2]
However, if we consider the motion of an object containing many ordered particles (for example, with a recognisable size, shape, position, velocity and orientation), we encounter a different phenomenon. It is easy to tell the difference between the reversed and forward motions of a person, a horse, a growing plant, a cup falling from a table and breaking, and most other examples from everyday life. Another example is the free expansion of a gas that initially is confined to one side of a box by a membrane. If the membrane is broken, the gas immediately expands into the other side (initially assumed to be evacuated), and we can easily tell the time reversed motion from the forward motion. In all of these cases, the motion at the individual molecule level is time reversal invariant, but it is clear that the gross motion of the macroscopic object is not.
Our question now is, “Why does nature seem to be time reversal invariant at the individual, or few, particle level, but apparently not at the level of many particles contained in an ordered system such as any common macroscopic object?”. In classical physics, irreversibility is always due to the second law of thermodynamics, which determines the forward direction of time. The entropy of a system of a moving horse or person, gravitational force, earth, and surroundings increases with time because the motion dissipates energy and increases the disorder in the body, earth and surroundings. The forward direction of a falling cup is apparent after the cup hits the floor and breaks because the broken cup is more disordered (has higher entropy) than the unbroken cup. However, even before the cup breaks, the entropy of the combined system of cup, gravitational force and earth increases as the cup falls.
Question
How is it possible that the entropy of a system of falling cup, gravitational force and earth increases even before the cup breaks? Assume that the earth is a collection of a large number of particles that are in thermal equilibrium at all times, i.e., that the energy of tidal motion is constantly being converted into heat energy.
# 2.4. Electromagnetism
French physicist Charles Augustin de Coulomb (1736–1806) discovered the force law obeyed by stationary, electrically charged objects between 1785 and 1791. In 1820, Danish physicist Hans Christian Oersted (1777–1851) discovered that an electric current produces a magnetic field, and that a magnetic field exerted a force on a current-carrying wire. From 1820 to 1827, French physicist Andre Ampere (1775–1836) extended these discoveries and developed the mathematical relationship describing the strength of the magnetic field as a function of current. In 1831, English chemist and physicist Michael Faraday (1791–1867) discovered that a changing magnetic field, which he explained in terms of changing magnetic lines of force, produces an electric current in a wire. This was a giant step forward because it was the forerunner of the concept of force fields, which are used to explain all forces in nature today.[3]
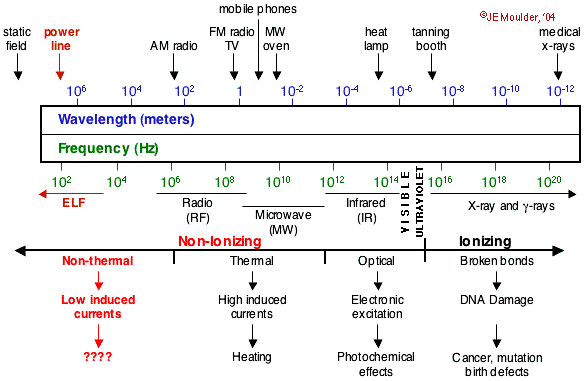
In 1873, these disparate phenomena and theories were all pulled together into one elegant theory by Scottish physicist James Clerk Maxwell (1831–1879). Maxwell’s four equations describing the electro-magnetic field are recognised as one of the greatest achievements of nineteenth century physics. Maxwell was able to calculate the speed of propagation of the electro-magnetic field from his equations, and found it to be approximately equal to the speed of light. He then proposed that light is an electro-magnetic phenomenon. Because electro-magnetic fields can oscillate at any frequency, he concluded that visible light occupied only a very small portion of the frequency spectrum of electro-magnetic radiation. The entire spectrum includes radio waves of low-frequency, high-frequency, very-high frequency, ultra-high frequency and microwaves. At still higher frequencies are infrared radiation, visible light, ultraviolet radiation, x-rays and gamma rays. All of these are fundamentally the same kind of waves, the only difference between them being the frequency of the radiation (see next section).
Now we ask, what is the electro-magnetic field, anyway? Is it a physical object? To answer that question, we must understand what we mean by the term physical object. One definition is that it is anything that carries force, energy and momentum. By this definition the electro-magnetic field is a physical object because it carries force, energy and momentum. However, this merely defines the electro-magnetic field in terms of other things that require their own definitions. Force, energy and momentum can only be defined in terms of the operations necessary to measure them and these operations require physical objects on which to make the measurements. Thus, all physical objects are defined in terms of other physical objects, so the definition is circular. This is another indication that the concept of objective reality is nothing but a concept (see Section 1.1).
# 2.5. Waves
In the 1800s, it was known that light had a wave-like nature, and classical physics assumed that it was indeed a wave. Waves are travelling oscillations. Examples are water waves, which are travelling surface oscillations of water; and waves on a tightly stretched rope, which are travelling oscillations of the rope. Waves are characterised by three parameters: wavelength (λ), oscillation frequency (f) and velocity (v).
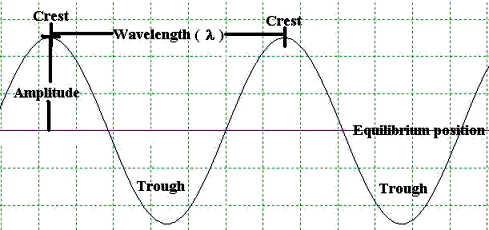
These parameters are related by the following equation:
The electro-magnetic spectrum (see previous section) contains electro-magnetic waves of all frequencies and wavelengths:
Waves are demonstrated at General Physics Animatons - Surendranath.B. Menu → Waves → Transverse Waves; and Sound & Waves — PhET Simulations (Table of Contents→Science Trek→Catch the Wave).
It was not known what the oscillating medium was in the case of light, but it was given the name ‘ether’. Maxwell had assumed that the ether provided an absolute reference frame with respect to which the velocity of any object or wave could be measured.
In 1881, German-American physicist Albert Michelson (1852–1931) and American physicist Edward Morley (1828–1923) performed ground-breaking experiments on the velocity of light. They found that the velocity of light on the earth always had the same constant value regardless of the direction of motion of the earth about the sun. This violated the concept, which was prevalent at the time, that the measured velocity of any object, be it particle or wave, depends on the observer’s velocity relative to the velocity of the other object. This concept is demonstrated in everyday life when our perception of another car’s velocity depends on the velocity of our own car. Thus, the measured velocity of light relative to the ether was expected to depend on the direction of motion of the earth relative to the velocity of the ether. But, the constancy of the velocity of light meant that the concept of the ether had to be abandoned because the ether velocity could not be expected to change with the observer’s velocity in just such a way that the velocity of light always had the same value. Thus, in the case of light waves, physicists concluded that there is no material medium that oscillates.
Question
Give some examples of waves whose observed velocities depend on the observer velocity.
Give some examples of waves whose observed velocities do not depend on the observer velocity.
# 2.6. Relativity
Implicit in the preceding discussion of classical physics was the assumption that space and time were the contexts in which all physical phenomena took place. Until 1905, physicists assumed that space and time were absolute in the sense that no physical phenomena or observations could affect them, therefore they were always fixed and constant. Newton thought this assumption was necessary for his laws of motion to be valid and until 1905, no physicist doubted its validity.
In 1905, the German-Swiss-American physicist Albert Einstein (1879–1955) revolutionised these ideas of time and space by publishing his theory of special relativity. (‘Special’ means that all motions are uniform, i.e., with constant velocity.) In this theory, he abandoned the concept of the ether, and with it the concept of the absolute motion of an object, realising that only relative motion between objects could be measured. Using only the assumptions that the observed velocity of light in free space is constant, and that the laws of motion are the same in all reference frames moving with constant velocity, he showed that neither length nor time is absolute. This means that both length and time measurements depend on the relative velocities of the observer and the observed.
An observer standing on the ground measuring the length of an airplane that is flying by will obtain a minutely smaller value than that obtained by an observer in the airplane. An observer on earth comparing a clock on a spaceship with a clock on earth will see that the spaceship clock moves slower than the earth clock. (Of course, an observer on the spaceship sees the earth clock moving slower than his clock! This is the famous twin paradox. It is resolved by realising that, when the spaceship returns to earth, the spaceship observer and clock will have aged less than the earth observer and clock. The difference between the two observers is that the spaceship has undergone deceleration in order to come to rest on earth. This deceleration, which is negative acceleration, is non-uniform motion; therefore special relativity does not apply.)
For an object having a non-zero rest mass, the special theory produced the famous relationship between the total energy (E) of the object, which includes its kinetic energy, and its mass (m):
where c is the speed of light in a vacuum. Einstein’s special theory has been confirmed by thousands of experiments, both direct and indirect.
In Einstein’s special theory of relativity, even though space and time were no longer absolute, they were still Euclidean. This meant that two straight lines in space–time (e.g., in an x, y, z, t co-ordinate system) which were parallel at one point always remained parallel no matter what the gravitational forces were.
Question
Suppose there is an ether. How would that affect Einstein’s special theory of relativity?
Question
Suppose the special theory of relativity had been proven wrong. What would be the effect on your life now?
In 1915, Einstein completed his greatest work, the general theory of relativity. Whereas the special theory deals with objects in uniform relative motion, i.e., moving with constant speed along straight lines relative to each other, the general theory deals with objects that are accelerating with respect to each other, i.e., moving with changing speeds or on curved trajectories. Examples of accelerating objects are an airplane taking off or landing, a car increasing or decreasing its speed, an elevator starting up or coming to a stop, a car going around a curve at constant speed, and the earth revolving around the sun or the moon revolving around the earth at constant speed.
A particularly important example of acceleration is that of an object free-falling in the earth’s gravity. A free-falling object is one that is acted upon only by the gravitational force, without air friction or other forces. All free-falling objects at the same spot in the earth’s gravitational field fall with the same acceleration, independent of the mass or material of the object. A free-falling object, such as an astronaut in a spaceship, does not experience a gravitational force (i.e., he experiences weightlessness), hence we can say that the acceleration of free-fall cancels out the gravitational force. Another way to state this fact is that a gravitational force is equivalent to an acceleration in the same direction. This is Einstein’s famed equivalence postulate, which he used in inventing general relativity.
The equivalence postulate applies to all objects, even light beams. Consequently, the path of a light beam is affected by a gravitational field just like the trajectory of a baseball. However, because of the very high speed of the photons in a light beam (3 x 108 metres per second, or 186,000 miles per second), their trajectories are bent by only very tiny amounts in the gravitational fields of ordinary objects like the sun.
Because all types of objects are affected in exactly the same way by gravity, an equivalent way of looking at the problem is to replace all gravitational forces by curved trajectories. The curved trajectories are then equivalent to curving space itself! This is the second key concept that Einstein used in the general theory of relativity. The result is that the general theory replaces the concept of gravity with the curvature of space. The curvature of a light beam around an individual star or galaxy is very small and difficult to measure. Even the whole universe curves the trajectory of a light beam only a little.
Question
Near the earth, how is space curved — towards the earth, away from the earth, or not at all?
Clear evidence that the force of gravity is nothing but a concept is given by the fact that it can be replaced by another concept, the concept of the curvature of space. Less clear is that the body sensations that we normally associate with the force of gravity (see Section 2.2) are also purely mental. We shall see more generally what we mean by the mind in Section 9.2.
General relativity also predicts the existence of black holes, objects that are so massive but so tiny that space around them curves into them. A light beam that gets close enough to a black hole will be bent into the black hole and never escape.
A fundamental feature of general relativity is that it predicts that matter, energy, space and time depend on each other and evolve together so that space and time are not independent quantities. But, what are they, anyway? In the same way that we said in Section 2.4 that the electro-magnetic field is nothing but a concept, and we said above that gravity is nothing but a concept, we can now say that space and time are also nothing but concepts! Space is a concept that allows us to conceptualise the separation of objects (which are nothing but concepts) and allows us to predict the trajectories of light beams (which are also nothing but concepts). Time is a concept that allows us to conceptualise how objects change (with time!). We shall say much more about conceptualisation in Section 9.2, and the conceptualisation of space and time in Chapter 12.
The average mass density of the universe cannot be measured directly because we are unable to see matter that is not emitting light, so the average mass density in a galaxy, for example, must be calculated from the trajectories of the motion of visible stars in the galaxy. Such measurements indicate that there is a large amount of matter in the universe that does not shine with its own or reflected light. This is called dark matter.
In 1929, fourteen years after Einstein published his general theory of relativity, American astronomer Edwin Hubble (1889–1953) discovered that the universe is expanding. Until 1998, it was assumed that the expansion rate is constant, but in 1998 it was discovered that the universe is actually expanding at an increasing rate rather than a constant one. This acceleration cannot be explained if the universe contains only ordinary and dark matter because these produce a gravitational force which is attractive, whereas an accelerating expansion requires a repulsive force. This repulsive force represents a ‘dark energy’ density in addition to the energy densities of ordinary and dark matter. Both dark matter and dark energy are presently being intensively investigated theoretically and experimentally because they could be the result of new physical laws operating.
Speaking of the universe as a whole, what are the effects of curved space? An important effect is that light beams no longer travel in straight lines. Hence, if two light beams start out parallel, they will eventually either converge or diverge. If they diverge, we say that space has negative curvature, and if they converge, we say that it has positive curvature. Zero curvature corresponds to parallel light beams always remaining parallel. This implies a Euclidean, or flat, space.
On February 11, 2003, C.L. Bennett and D.N. Spergel reported[4] a new map of the early universe as recorded by NASA’s WMAP satellite. By measuring minute temperature non-uniformities in the cosmic microwave background, researchers deduced that only 4% of the universe is ordinary matter, while 23% is cold dark matter, and 73% is dark energy. These data, refined by quasar measurements in 2004, indicated that the universe is flat and that its age is 13.7±0.2 billion years, the most accurate measurement to date. However, this estimate of the curvature depended on the assumption that the universe is expanding at a constant rate.
There are powerful theoretical reasons for believing that the curvature of our space is neither positive nor negative but is exactly zero. The curvature depends on the average energy density (the average amount of energy per cubic metre), the expansion rate of the universe and the rate of increase in the expansion rate. In practice, it is too difficult to measure the curvature by measuring the curvature of light beam trajectories, but it can be estimated if the average angular size of the intensity spots in the cosmic microwave background, the expansion rate of the universe, and the rate of increase in the expansion rate are all known.[5]
Side note
In his initial papers, Einstein had constructed a model of the universe with zero curvature that was not expanding at all. Later, in 1922 but also before Hubble’s discovery, Russian physicist Aleksandr Friedmann (1888–1925) discovered solutions to the general relativity equations that described an expanding universe with either positive or negative curvature. Still later, in 1932 after Hubble’s discovery, Einstein and W. de Sitter constructed a model that described an expanding universe with zero curvature.
Question
Suppose there was no dark matter. What would be the observable result?
Question
Suppose there was no dark energy. What would be the observable result?
In inventing the special theory of relativity, Einstein was heavily influenced by the positivism of Austrian natural philosopher Ernst Mach (1838–1916). Positivism is the philosophy that states that the only authentic knowledge is knowledge that is based on actual sense experience. This attitude is derived from the belief that the only objective, external reality that exists is one that can be directly observed with the senses, such as macroscopic objects. In inventing and explaining the special theory, Einstein followed the positivist approach and made extensive use of the empirical definitions of measurements of time and space, and he incorporated those definitions into the mathematics, which describe how length and time vary with the relative velocity of observer and observed. In this way, Einstein was able to avoid the concept of space except as being the context of measurements of length and time.
However, Einstein abandoned positivism when he developed the general theory of relativity, and it is unlikely that he could have developed it without doing so. His concept of general relativity depended essentially on an intuitive leap from the empirical operations of measuring the force of gravity and the accelerations of objects to a theoretical model of space which was curved and in which there were no gravitational forces. He likely could not have done this without believing that space was objectively real rather than being merely the context for making measurements of length and time.
Question
Suppose the general theory of relativity had been proven wrong. What would be the effect on your life now?
In addition to curved space, a physicist who adhered to the positivist philosophy would not have conceived the electron, the atom or quantum waves. Einstein’s intuitive leap is an example of an essential aspect of the work of scientists. The individual experiments that scientists perform are always very specific to a particular problem in particular circumstances. Any attempt to comprehend the results of many such experiments on many similar topics would be futile without some kind of unifying model that is presumed to represent some aspect of the external, objective reality affecting those experiments.
For example, force fields are theoretical models of gravitational or electro-magnetic forces, and curved space–time is a model of space–time that accounts for the gravitational force. There are other models that account for the weak and strong forces that act on elementary particles. And there are models of the nucleus, the atom, molecules, crystals and gases. All of these models are highly mathematical because mathematics is the universal language of physics.
When a model is found that accurately accounts for experimental observations, there is a strong tendency to think of the model itself as the external, objective reality. Thus, both physicists and the general public routinely speak of elementary particles, nucleï, atoms and space–time as being real objects, rather than simply as mathematical models. We shall see later that this tendency creates intractable problems in trying to understand the true nature of Reality.
Question
From your own experience alone, answer the question, “What is space, anyway?”.
In classical physics, objects interact with each other through their force fields, which are also objects in external, objective reality. For example, the atoms and molecules in a solid, liquid or gas are held together by the electro-magnetic force. Charged particles also interact through the electro-magnetic force. It turns out that all physical objects, which are nothing but concepts, interact with each other through their force fields, which are also nothing but concepts (see Section 2.4).

As revolutionary as Einstein’s general theory of relativity was, it did nothing to change the belief that we as observers still live within the context of space–time even though space–time is no longer thought to be absolute and unchanging. This means, for example, that we as objects are still subject to the experience of separation and isolation from other objects, and to the experience of ageing and the ultimate death of the body. It took an even more revolutionary theory, the quantum theory, to begin to shake these imprisoning beliefs.
Questions
What is the Hubble viewing? Stars? Galaxies? Space? A mathematical concept? Consciousness? Ourselves? Nothing?
Questions
From your own experience, and with a minimum of concepts, be as specific and as accurate as possible in answering the following questions. Avoid the use of simple synonyms. What is the gravitational force? An example of an unsuitable answer is “a force that pulls me down and holds me to my chair”. This example offends by repeating the word ‘force’ and it uses the concepts ‘pulls’, ‘me’, ‘down’, ‘holds’, ‘my’ and ‘chair’. Another unsuitable answer is “curved space” because it is a synonym and is not an experience.
# Footnotes
Gas Properties - Ideal Gas Law | Kinetic Molecular Theory | Diffusion - PhET Interactive Simulations ↩︎
A computer simulation of the force on an electric charge is given at Electric Field of Dreams - Electricity | Electric Charges | Electric Field - PhET Interactive Simulations ↩︎
Science News, February 15, 2003 ↩︎
The fate of the cosmos: Dark energy can shape the universe ↩︎